Creating a Usable Hellschreiber Font
After my previous success transmitting Hellschreiber with my gate driver-based amplifier, I thought I’d flesh things out in more detail. One thing I needed to figure out was how I am going to store the font for transmitting arbitrary text using Hellschreiber.
Hellschreiber Details
This mode uses CW, FSK, PSK, etc., to transmit a series of pixels. When transmitting in one state, there is a white pixel, and in another state a black pixel. In a lot of graphics contexts, we tend to think of row-major pixel arrangements, but Rudolph Hell’s mechanical hellschreiber design is based around processing the data as columns of pixels. Often, the pixels are seen in columns of 14, and letters 7 pixels wide.

Hellschreiber pixel data is transmitted from bottom to top, one column after another. You might wonder how the receiver can tell when a new column starts. But this is the genius of Rudolph Hell’s system – there is no need for synchronization at all because the receiver simply renders two vertical copies of the incoming pixel data. This means that wherever the receiver’s printer is (bottom, middle, or top of a column), there will always be one legible column in the resulting two-column output. This gives hellschreiber its characteristic appearance, and in my opinion is a very elegant and simple solution to the challenge of synchronization:
So to make a general-purpose hellschreiber transmitter, I need to encode a font that is conducive to this sort of pixel arrangement. Further, I’d like it to be compact, since I have to store this in a microcontroller (arduino, etc.).
Minimalistic Pixel Font
For better or worse, my previous experiments have used a 5x7 font instead of the traditional 7x14. People choose all kinds of things font-wise, and I don’t know how much it matters to use a full-size font. I do notice that the bolder, wider fonts seem to be more resilient against interference on the air, and in my initial testing the 5x7 font seemed quite reasonable. Perhaps in the future, I’ll repeat this process with a higher-resolution font if it seems necessary.
In my last blog post, I arranged my font data manually with byte values in a two-dimensional array as follows:
byte alpha[6][7][7] = {
{ {0, 0, 0, 0, 0},
{0, 1, 0, 0, 1},
{0, 1, 1, 0, 1},
{0, 1, 0, 1, 1},
{0, 1, 0, 0, 1},
{0, 1, 0, 0, 1},
{0, 0, 0, 0, 0} },
. . .
This is laborious, inefficient, and it’s not very obvious what the font actually looks like. I found myself running it, demodulating the result, and realizing I had to move pixels around. It’s just not the “right way” to do this. I decided it would be better to make the font in a normal graphics program (e.g., Gimp), and write a program to encode it for inclusion in my firmware.
And there’s no real need to draw my own font. I’d had one lying around from experiments writing retro game engines (where every pixel matters!). I really don’t know where I found this one (if someone reads this and knows its origin, let me know, I’ll cite a reference!), but I started with this 5x7 pixel font:

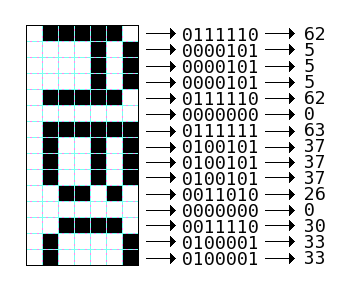
Since hellschreiber conceives of the font in columns, from bottom to top, I simply rotated the image by 90 degrees and saved it as a PNM that is easy to process. Each column of the font is 7 pixels, and the pixels are either black or white; so it is an obvious fit to store each column as a one byte bitmask. For example, the letter A shown below can be encoded as the values 62, 5, 5, 5, 62:
Automating Font Generation
I really didn’t want to manually encode all of these pixel columns as bitmasks by hand! It would take forever, and if I needed to change the font, it would be frustrating to manually decode and replace values in the future. Since I have an image of the font, I should be able to write a program that processes that data and automatically generates the font encoding.
If you look closely at the font image above, you’ll notice that most of the characters are 6 pixel columns wide, with a blank column (all white pixels) in between. But some of them are not… e.g., the letter ‘I’ is only three columns wide. So this is actually a variable-width font, oops! But it looks pretty nice, and there’s nothing wrong with a variable width font in hellschreiber (it just needs to be human readable). So I decided to embrace it, rather than to take all the odd-length characters and square them up.
Since each character is separated by a blank row, it’s pretty easy to identify the boundaries. I wrote a program that reads the pixel data in my rotated image, one row at a time. It converts each one to a bitmask, and stores a detected character every time it encounters one of these blank spaces. The only wrinkle is that the double-quote character (“) ends up parsing as two single ticks. This is an acceptable flaw, actually, which I’ll get to later.
This font file, then, gives me a list of bitmasks for all the characters. But it’s not in ASCII order, for example, so I needed to come up with a way to associate the ASCII characters a user might provide as a message with the appropriate items in the list of bitmasks. There isn’t really a “good” way to dot his, so I did what works pragmatically – I typed out the contents of the font image in a string, and used this to create an array of offsets for a full 7-bit ASCII table.
(defparameter *key*
"ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789.,\"''?!@_*#$%&()+-/:;<=>[\\]^`{|}")
(defun font-char (char)
(let ((pos (position char *key*)))
(when pos
(letter *pixels* *widths* pos))))
So the result is two arrays – one array is a listing of the font column bitmasks, with blank columns as separators; and the second array is an ASCII table of indexes into the array of bitmasks. If a character doesn’t exist in the font, then its index is -1, so the transmitter firmware can take appropriate action.
The program that generates this output from the font image is written in Common Lisp (because that was my mood that day), and you can read the program here. It’s not beautiful code, but I don’t have to run it very often. It was still easier to do it this way than to construct the font data structures by hand.
The Resulting Font Data
So the output of this encoding process is as follows – two fairly svelte arrays that make hellschreiber transmission pretty convenient:
// Hellschreiber 5x7 font
// ASCII table of offsets into column bit-mask table
short font_offsets[] = {
/* 0 */ -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
/* 16 */ -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
/* 32 */ -1, 375, 363, 393, 399, 405, 411, 365, 417, 420, 389, 423, 361, 429, 359, 435,
/* 48 */ 301, 307, 311, 317, 323, 329, 335, 341, 347, 353, 439, 441, 443, 449, 455, 369,
/* 64 */ 377, 0, 6, 12, 18, 24, 30, 36, 42, 48, 52, 58, 64, 70, 76, 82,
/* 80 */ 88, 94, 100, 106, 112, 118, 124, 130, 136, 142, 148, 461, 464, 468, 471, 383,
/* 96 */ 475, 154, 160, 166, 172, 178, 184, 190, 196, 202, 204, 208, 214, 217, 223, 229,
/* 112 */ 235, 241, 247, 253, 259, 265, 271, 277, 283, 289, 295, 478, 482, 484, -1, -1 };
// column bit-masks, bottom to top from 7th bit, big-endian
byte font_columns[] = {
/* 0 */ 62, 5, 5, 5, 62, 0, 63, 37, 37, 37, 26, 0, 30, 33, 33, 33,
/* 16 */ 33, 0, 63, 33, 33, 33, 30, 0, 63, 37, 37, 37, 33, 0, 63, 5,
/* 32 */ 5, 5, 1, 0, 30, 33, 37, 37, 29, 0, 63, 4, 4, 4, 63, 0,
/* 48 */ 33, 63, 33, 0, 32, 32, 33, 31, 1, 0, 63, 8, 4, 10, 49, 0,
/* 64 */ 63, 32, 32, 32, 32, 0, 63, 2, 4, 2, 63, 0, 63, 2, 4, 8,
/* 80 */ 63, 0, 30, 33, 33, 33, 30, 0, 63, 5, 5, 5, 2, 0, 30, 33,
/* 96 */ 41, 17, 46, 0, 63, 5, 5, 5, 58, 0, 34, 37, 37, 37, 25, 0,
/* 112 */ 1, 1, 63, 1, 1, 0, 31, 32, 32, 32, 31, 0, 7, 24, 32, 24,
/* 128 */ 7, 0, 31, 32, 28, 32, 31, 0, 49, 10, 4, 10, 49, 0, 1, 2,
/* 144 */ 60, 2, 1, 0, 49, 41, 37, 35, 33, 0, 16, 42, 42, 42, 60, 0,
/* 160 */ 63, 34, 34, 34, 28, 0, 28, 34, 34, 34, 34, 0, 28, 34, 34, 34,
/* 176 */ 63, 0, 28, 42, 42, 42, 12, 0, 4, 62, 5, 5, 1, 0, 12, 82,
/* 192 */ 82, 82, 62, 0, 63, 2, 2, 2, 60, 0, 61, 0, 64, 64, 61, 0,
/* 208 */ 63, 16, 8, 20, 34, 0, 31, 32, 0, 62, 2, 60, 2, 60, 0, 62,
/* 224 */ 2, 2, 2, 60, 0, 28, 34, 34, 34, 28, 0, 126, 34, 34, 34, 28,
/* 240 */ 0, 28, 34, 34, 34, 126, 0, 62, 4, 2, 2, 2, 0, 36, 42, 42,
/* 256 */ 42, 16, 0, 2, 31, 34, 34, 32, 0, 30, 32, 32, 32, 62, 0, 6,
/* 272 */ 24, 32, 24, 6, 0, 30, 32, 30, 32, 30, 0, 34, 20, 8, 20, 34,
/* 288 */ 0, 14, 80, 80, 80, 62, 0, 34, 50, 42, 38, 34, 0, 30, 33, 33,
/* 304 */ 33, 30, 0, 34, 63, 32, 0, 33, 49, 41, 37, 34, 0, 33, 33, 37,
/* 320 */ 37, 26, 0, 7, 4, 4, 63, 4, 0, 39, 37, 37, 37, 25, 0, 30,
/* 336 */ 37, 37, 37, 25, 0, 1, 1, 49, 13, 3, 0, 26, 37, 37, 37, 26,
/* 352 */ 0, 34, 37, 37, 37, 30, 0, 32, 0, 96, 0, 3, 0, 3, 0, 3,
/* 368 */ 0, 1, 1, 41, 5, 2, 0, 47, 0, 30, 33, 37, 43, 14, 0, 32,
/* 384 */ 32, 32, 32, 32, 0, 5, 2, 5, 0, 18, 63, 18, 63, 18, 0, 36,
/* 400 */ 42, 127, 42, 18, 0, 35, 19, 12, 50, 49, 0, 26, 37, 42, 16, 40,
/* 416 */ 0, 30, 33, 0, 33, 30, 0, 8, 8, 62, 8, 8, 0, 8, 8, 8,
/* 432 */ 8, 8, 0, 48, 12, 3, 0, 18, 0, 50, 0, 8, 20, 20, 34, 34,
/* 448 */ 0, 20, 20, 20, 20, 20, 0, 34, 34, 20, 20, 8, 0, 63, 33, 0,
/* 464 */ 3, 12, 48, 0, 33, 63, 0, 6, 1, 6, 0, 1, 2, 0, 4, 30,
/* 480 */ 33, 0, 63, 0, 33, 30, 4, 0 };
Transmitting a message is straightforward. Iterate through each character, look up the offset into the bitmask array. Actuate the transmitter to send each column sequentially until encountering a NULL value (the blank separator). The only wrinkle is double quote – it’s easy enough, though, to just transmit two apostrophes for any double quote. I suppose I could manually tack it on, but it’s not that big of a deal, and I’m OK with this special case for now. I’ll probably fix it some day.
Conclusions and Next Steps
With this in hand, I’m ready to test my next transmitter, once I have the amplifier built and measured for Part 97 compliance. My next post will include design, construction, and on-air testing of a full Hellschreiber transmitter!